2024智慧树网课答案 概率论与数理统计(温州医科大学) 最新完整智慧树知到满分章节测试答案
第一章 单元测试
1、 问题:在盒子中有4只白球,2只红球,从盒子中任取2只球(不放回抽样),则取得2只白球的概率是( )。
选项:
A:
B: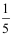
C: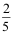
D:![]()
答案: 【
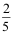
】
2、 问题:设A,B互不相容的事件,则( )。
选项:
A: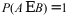
B: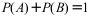
C:
D: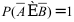
答案: 【
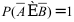
】
3、 问题:从0,1,2 ,9这10个阿拉伯数字中随意选8个(允许重复),组成一个8位电话号码(第一位不为0)。引进事件
,9这10个阿拉伯数字中随意选8个(允许重复),组成一个8位电话号码(第一位不为0)。引进事件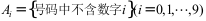 ,则下列各命题错误的是( )。
,则下列各命题错误的是( )。
选项:
A: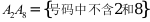
B: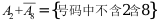
C: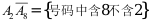
D: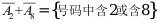
答案: 【
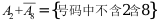
】
4、 问题: 甲、乙、丙3人独立地破译一种密码,他们能译出的概率分别是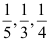 ,则能译出这种密码的概率是( )。
,则能译出这种密码的概率是( )。
选项:
A:![]()
B:
C:
D: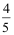
答案: 【

】
5、 问题:
袋中有3个白球2个红球,从中无放回地取3次,每次取1个球,则恰有两次取得白球的概率为( )。
选项:
A:
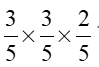
B:

C:
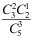
D:![]()
答案: 【
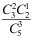
】
6、 问题:
设A,B为两个事件,且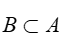 ,则下列结果正确的是( )。
,则下列结果正确的是( )。
选项:
A:
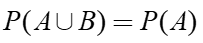
B: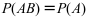
C: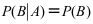
D: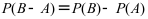
答案: 【
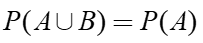
】
7、 问题:设事件A, B满足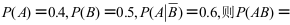 ( )。
( )。
选项:
A:0.3
B:0.1
C:0.05
D:0.2
答案: 【
0.1
】
8、 问题:设A和B互为对立事件,则下列各式不成立的是( )。
选项:
A: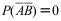
B: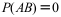
C: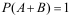
D: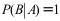
答案: 【
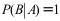
】
9、 问题:10把钥匙中有3把能打开门,今任取两把,则能打开门的概率( )。
选项:
A:
B:
C: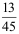
D:
答案: 【

】
10、 问题:某仓库有同样规格的产品8箱,甲,乙,丙3个厂各生产3箱,2箱和3箱。甲,乙,丙3个厂的次品率分别为 。现从8箱中任取1箱,再从取得的1箱中任取1件,则取得次品的概率是( )。
。现从8箱中任取1箱,再从取得的1箱中任取1件,则取得次品的概率是( )。
选项:
A:![]()
B:![]()
C:![]()
D:![]()
答案: 【
![]()
】
11、 问题:盒内有7个球,其中红球4个,白球3个,不放回地一个一个往外取球,则第三次才取到白球的概率与第三次取球时取到白球的概率分别为( )。
选项:
A: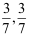
B:![]()
C:![]()
D:![]()
答案: 【
![]()
】
12、 问题: 两批同型产品分别来自甲、乙两个工厂,甲厂产品共6件,其中一等品2件;乙厂产品共4件,其中一等品1件,先从甲厂产品中任取1件混入到乙厂产品中,再从后者任取1件,则它是一等品的概率为( )。
选项:
A:![]()
B: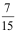
C: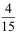
D: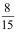
答案: 【
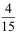
】
13、 问题:设事件A,B相互独立,A,C互不相容,且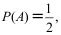
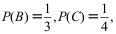
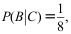 则概率
则概率 ( )。
( )。
选项:
A: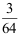
B:
C:![]()
D:![]()
答案: 【
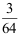
】
14、 问题:
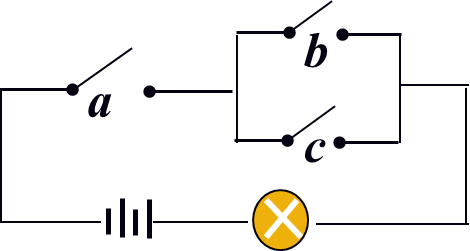
如图所示的电路中,设事件A,B,C分别表示电路开关a, b, c闭合,且事件D表示“指示灯亮”,则用A,B,C表示 “指示灯亮”( )。
选项:
A:
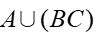
B:
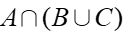
C:

D:
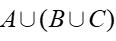
答案: 【
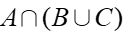
】
15、 问题: 一个家庭生两个孩子,已知其中一个是女孩,则另一个是女孩的概率为( )。
选项:
A:![]()
B: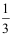
C:![]()
D:
答案: 【
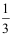
】
16、 问题:若n(>2)个事件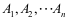 相互独立,则下列结论错误的是( )。
相互独立,则下列结论错误的是( )。
选项:
A: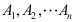 任意两个事件相互独立
任意两个事件相互独立
B: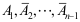 相互独立
相互独立
C: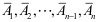 不一定相互独立
不一定相互独立
D:n个事件相互独立和两两独立是不同的
答案: 【
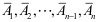 不一定相互独立
不一定相互独立
】
17、 问题:设A与B是两个事件,已知P(A)=0.3,P(B)=0.2,P(AB)=0.1,则 =( ) 。
=( ) 。
选项:
A:0.4
B:0.5
C:0.6
D:0.9
答案: 【
0.6
】
18、 问题:设事件A与B,已知P(A)=0.3,P(B)=0.6,P(AB)=0.2则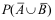 是( ) 。
是( ) 。
选项:
A:0.9
B:0.8
C:0.7
D:0.3
答案: 【
0.8
】
19、 问题:三个人独立地各投篮一次,设命中率分别为0.3,0.5,0.7,则恰好投中2次概率为( )。
选项:
A:0.915
B:0.813
C:0.724
D:0.395
答案: 【
0.395
】
20、 问题:掷一对骰子,则2个骰子点数总和是6的概率是 ( )。
选项:
A:![]()
B: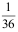
C:![]()
D: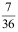
答案: 【
![]()
】
21、 问题:
已知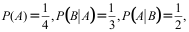 则下列结论正确的是( )。
则下列结论正确的是( )。
选项:
A:
B:
C:
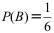
D:
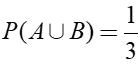
答案: 【


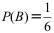
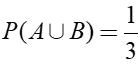
】
22、 问题:乙两人独立地对同一目标射击一次,其中命中率分别为0.6和0.5。设目标被击中的概率为p;现已知目标被击中,则它是甲击中的概率为q, 则下列结论正确的是( )。
选项:
A:
B:![]()
C:![]()
D:![]()
答案: 【
![]()
![]()
】
23、 问题:设P(A)>0, P(B)>0, 且事件A,B相互独立,则下列结论正确的是( )。
选项:
A:事件A的发生不影响事件B的发生概率,即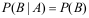
B:事件B的发生不影响事件A的发生概率,即
C:
D:事件A、B不可能互不相容
答案: 【
事件A的发生不影响事件B的发生概率,即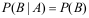
事件B的发生不影响事件A的发生概率,即

事件A、B不可能互不相容
】
24、 问题:
关于德摩根定律下列正确的是( )。
选项:
A: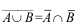 的含义是“A,B至少有一个发生”的对立事件是“A,B都不发生”
的含义是“A,B至少有一个发生”的对立事件是“A,B都不发生”
B: 中还可以得到“A,B都不发生” 的对立事件是“A,B至少有一个发生”
中还可以得到“A,B都不发生” 的对立事件是“A,B至少有一个发生”
C: 的含义是“A,B都发生”的对立事件是“A,B至少有一个不发生”
的含义是“A,B都发生”的对立事件是“A,B至少有一个不发生”
D:
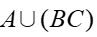 中还可以得到“A,B至少有一个不发生”的对立事件是“A,B都发生”
中还可以得到“A,B至少有一个不发生”的对立事件是“A,B都发生”
答案: 【
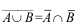 的含义是“A,B至少有一个发生”的对立事件是“A,B都不发生”
的含义是“A,B至少有一个发生”的对立事件是“A,B都不发生”
 中还可以得到“A,B都不发生” 的对立事件是“A,B至少有一个发生”
中还可以得到“A,B都不发生” 的对立事件是“A,B至少有一个发生”
 的含义是“A,B都发生”的对立事件是“A,B至少有一个不发生”
的含义是“A,B都发生”的对立事件是“A,B至少有一个不发生”
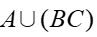 中还可以得到“A,B至少有一个不发生”的对立事件是“A,B都发生”
中还可以得到“A,B至少有一个不发生”的对立事件是“A,B都发生”
】
25、 问题:
用A、B、C表示A、B、C至少有一个发生为ABC。( )
选项:
A:对
B:错
答案: 【
错
】
26、 问题:设 ,若事件A与B独立,则P(B)=0.5。( )
,若事件A与B独立,则P(B)=0.5。( )
选项:
A:对
B:错
答案: 【
对
】
27、 问题:对于事件A和B,
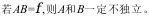 ( )
( )
选项:
A:对
B:错
答案: 【
对
】
28、 问题:若 两两互不相容,对任意一事件A,则
两两互不相容,对任意一事件A,则 也两两互不相容。( )
也两两互不相容。( )
选项:
A:对
B:错
答案: 【
对
】
29、 问题:一批产品共有10个正品和2个次品,任意抽取两次,每次抽1个,抽出后不再放回,则第二次抽出的是次品的概率为 。( )
。( )
选项:
A:对
B:错
答案: 【
错
】
第二章 单元测试
1、 问题: 设每次试验成功的概率为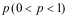 ,重复进行试验直到第
,重复进行试验直到第![]() 次才取得成功的概率为( )。
次才取得成功的概率为( )。
选项:
A:
B:
C: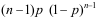
D: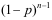
答案: 【

】
2、 问题: 设随机变量X的分布函数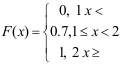 , 则X的概率分布律( )。
, 则X的概率分布律( )。
选项:
A:
B:
C:
D: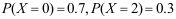
答案: 【

】
3、 问题: 设X的概率密度函数为 ,则X的分布函数为( )。
,则X的分布函数为( )。
选项:
A:
B:
C: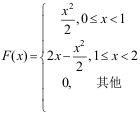
D:都不对
答案: 【

】
4、 问题:设离散型随机变量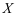 服从于参数为
服从于参数为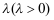 的泊松分布,已知
的泊松分布,已知 ,则参数
,则参数![]() ( )。
( )。
选项:
A:1
B:![]()
C:6
D: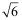
答案: 【
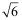
】
5、 问题:设随机变量![]() 的概率密度为
的概率密度为 ,则
,则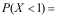 ( )。
( )。
选项:
A:![]()
B: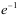
C:![]()
D: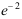
答案: 【
![]()
】
6、 问题:机变量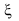 的概率密度为
的概率密度为 ,若
,若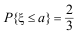 ,则
,则![]() =( )。
=( )。
选项:
A:4.2
B:5.4
C:6.5
D:7.6
答案: 【
6.5
】
7、 问题: 设随机变量 ,且
,且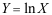 ,则Y的概率密度函数为( )。
,则Y的概率密度函数为( )。
选项:
A: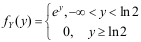
B: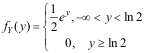
C:
D: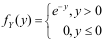
答案: 【
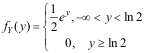
】
8、 问题:设 和
和![]() 分别是随机变量
分别是随机变量![]() 和
和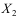 的分布函数,为使
的分布函数,为使 是某一随机变量的分布函数,在下列给定的各组数值中应取( )。
是某一随机变量的分布函数,在下列给定的各组数值中应取( )。
选项:
A: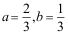
B:
C:
D: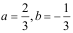
答案: 【
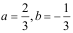
】
9、 问题:若离散型随机变量X的分布律为 ,又Y=2X+1,则P{Y>4}=( )。
,又Y=2X+1,则P{Y>4}=( )。
选项:
A:0.3
B:0.2
C:0
D:0.5
答案: 【
0.5
】
10、 问题:某生产线生产玻璃制品,生产过程中玻璃制品常出现气泡,以致产品成为次品。设次品率为p=0.001。 现取8000件产品,利用泊松分布近似,则其中次品数小于7的概率p=( )(设各产品是否为次品相互独立)。
选项:
A:
B:
C: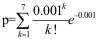
D: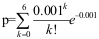
答案: 【

】
11、 问题:根据标准正态分布的概率密度函数性质知: 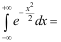 ( )。
( )。
选项:
A: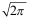
B: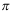
C:![]()
D:1
答案: 【
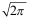
】
12、 问题:设![]() 为某正态分布的概率密度函数,
为某正态分布的概率密度函数,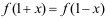 ,
,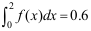 ,则
,则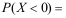 ( )。
( )。
选项:
A:0.3
B:0.4
C:0.2
D:0.6
答案: 【
0.2
】
13、 问题:设随机变量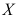 服从正态分布
服从正态分布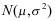 (
( ![]() ), 且关于x的一元二次方程
), 且关于x的一元二次方程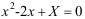 有实根的概率为
有实根的概率为![]() ,则
,则![]() =( )。
=( )。
选项:
A:1
B:2
C:-2
D:-1
答案: 【
1
】
14、 问题:设空调的寿命(以年计) ,已知一空调已使用了5年,则其寿命不超过8年的概率为( )。
,已知一空调已使用了5年,则其寿命不超过8年的概率为( )。
选项:
A: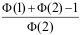
B: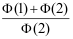
C:
D: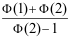
答案: 【
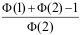
】
15、 问题:设随机变量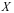 服从正态分布
服从正态分布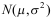 ,且
,且 ,则下列正确的是( )。
,则下列正确的是( )。
选项:
A:p随着µ的增加而减加
B:p随着ϭ的增加而增加
C:p随着µ的增加而增小
D:p随着ϭ的增加而减小
答案: 【
p随着ϭ的增加而增加
】
16、 问题:设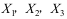 是3个随机变量,且
是3个随机变量,且 ,
,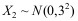 ,
,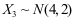 ,
, 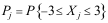
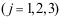 ,则
,则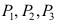 中最大是 ( )。
中最大是 ( )。
选项:
A:![]()
B: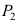
C: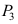
D:不能判断
答案: 【
![]()
】
17、 问题:设一批产品有15件,其中5件次品,10件正品,现从这批产品中任取5件,若用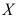 表示取出的5件产品中的次品件数,则
表示取出的5件产品中的次品件数,则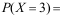 ( )。
( )。
选项:
A:![]()
B:![]()
C: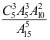
D: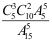
答案: 【
![]()
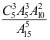
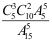
】
18、 问题:设随机变量X在区间[2,5]上服从均匀分布,对X进行的两次独立观测中,至少有一次的观测值大于3的概率为( )。
选项:
A: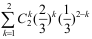
B: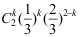
C: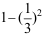
D: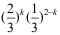
答案: 【
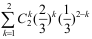
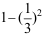
】
19、 问题:已知连续型随机变量X的分布函数为 ,则下列结论正确的是( )。
,则下列结论正确的是( )。
选项:
A:![]()
B:![]()
C:
D: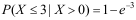
答案: 【
![]()
![]()

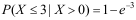
】
20、 问题:一盒中有3个黑球,2个红球,采用放回式抽样,共取了X次才首次取到红球,则下列结论正确的是( )。
选项:
A:X的分布律为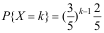
B:X的分布律为
C: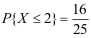
D:
答案: 【
X的分布律为
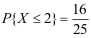

】
21、 问题:若X的所有可能取值是集合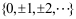 ,则X为离散型随机变量。( )
,则X为离散型随机变量。( )
选项:
A:对
B:错
答案: 【
对
】
22、 问题:掷一颗骰子100次,则“2点” 出现次数X的分布律为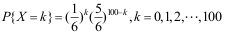 。( )
。( )
选项:
A:对
B:错
答案: 【
错
】
23、 问题:设X为连续型随机变量,则对于![]() , 有
, 有 。 ( )
。 ( )
选项:
A:对
B:错
答案: 【
对
】
24、 问题: ( )
( )
选项:
A:对
B:错
答案: 【
对
】
第三章 单元测试
1、 问题: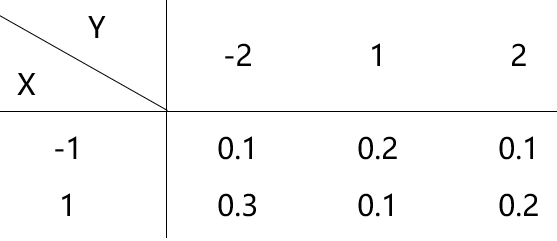
设二维随机向量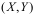 的联合分布律如图,且Z=min(X, Y),则Z的概率分布律为( )。
的联合分布律如图,且Z=min(X, Y),则Z的概率分布律为( )。
选项:
A: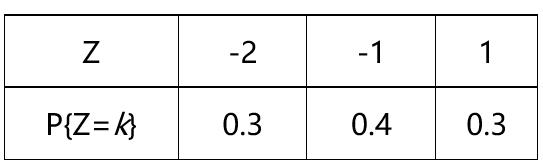
B: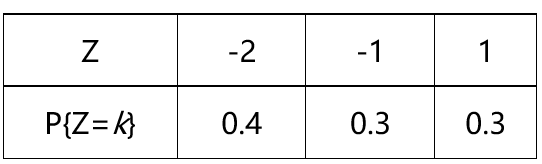
C: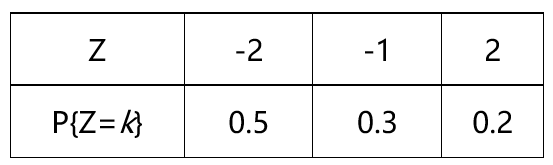
D: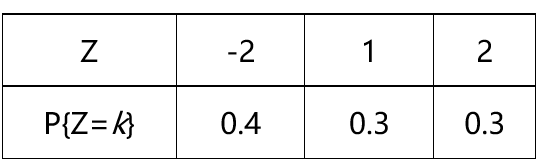
答案: 【

】
本文章不含期末不含主观题!!
本文章不含期末不含主观题!!
支付后可长期查看
有疑问请添加客服QQ 2356025045反馈
如遇卡顿看不了请换个浏览器即可打开
请看清楚了再购买哦,电子资源购买后不支持退款哦


