绪论 单元测试

1、 问题:

点解析和点可导是等价的。（ ）

选项：
A:对
B:错
答案: 【
错
】

第一章 单元测试

1、 问题:

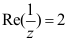 则为复平面上的（ ）。

选项：
A:圆
B:抛物线
C:双曲线
D:椭圆
答案: 【
圆
】

2、 问题:-1的幅角为（ ）。
选项：
A:0
B:π
C: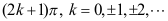
D:π/2
答案: 【

】

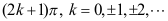
3、 问题:函数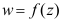 在点z₀及其邻域（ ），则称 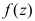在点z₀解析。
选项：
A:连续
B:可导
C:可积
D:极限存在
答案: 【
可导
】

4、 问题:函数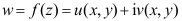 在点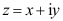 可导的必要条件是（ ）。
选项：
A:
B: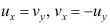
C: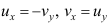
D: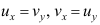
答案: 【

】

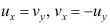
5、 问题:以复数z₀为圆心，以任意小的正实数ε为半径作一圆，则圆内所有点的集合称为z₀点的（ ）。
选项：
A:区域
B:邻域
C:边界
D:闭区域
答案: 【
邻域
】

6、 问题:复平面上以z₀为中心，内径为a外径为b的闭环域表示为（ ）。
选项：
A: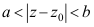
B: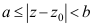
C: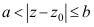
D: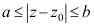
答案: 【

】

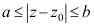
7、 问题:无源空间平面静电场的复势表示为 ，则下列表述中哪个不正确（ ）？
选项：
A:u(x,y)表示电力线，则v(x,y)表示电势
B: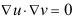
C:u(x,y)和v(x,y)互为共轭调和函数
D: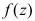 不一定是解析函数
答案: 【
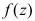不一定是解析函数
】

8、 问题:复数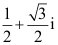 的主幅角为（ ）。
选项：
A:0
B:π/2
C:π/3
D:π
答案: 【
π/3
】

9、 问题:复数z的三种表示分别是（ ）。
选项：
A:代数表示
B:共轭表示
C:三角表示
D:指数表示
答案: 【
代数表示
三角表示
指数表示
】

10、 问题:关于复平面上的无穷大点，下面哪些说法是正确的（ ）.
选项：
A:复平面上一定存在一个和无穷大一一对应的点
B:无穷大的模是无穷大，幅角无意义
C:若z有限，则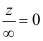
D:通过测地投影，复平面上的无穷大点映射到复球北极N
答案: 【
无穷大的模是无穷大，幅角无意义
若z有限，则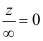
通过测地投影，复平面上的无穷大点映射到复球北极N
】

11、 问题:3.下面的复变函数中，是多值函数的有哪些（ ）？
选项：
A: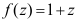
B: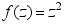
C: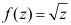
D:
答案: 【


】

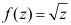
12、 问题:闭区域一定是区域。（ ）
选项：
A:对
B:错
答案: 【
错
】

13、 问题:区域边界线的正方向一定是逆时针方向。（ ）
选项：
A:对
B:错
答案: 【
错
】

14、 问题:C-R条件是复变函数可导的充要条件。（ ）
选项：
A:对
B:错
答案: 【
错
】

15、 问题:

点解析和点可导是等价的（ ）

选项：
A:对
B:错
答案: 【
错
】

16、 问题:u和v是区域B上共轭调和函数，则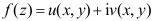 一定在B上解析。（ ）
选项：
A:对
B:错
答案: 【
错
】

第二章 单元测试

1、 问题:设C为从原点沿y²=x至1+i的弧段，则 （ ）。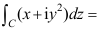
选项：
A: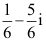
B: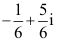
C: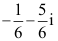
D: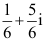
答案: 【

】

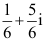
2、 问题:

设C为不经过点1和-1的正向简单闭合曲线，则图中为

选项：
A: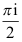
B: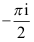
C:0
D:其他选项情况都有
答案: 【
其他选项情况都有
】

3、 问题:设c为任意实常数，那么由调和函数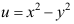 确定的解析函数 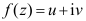是（ ）。
选项：
A:
B:
C: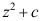
D: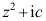
答案: 【

】

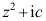
4、 问题:设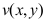 在区域B内为 的共轭调和函数，在下列函数在B内解析的函数是（ ）。
选项：
A:
B: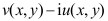
C: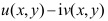
D: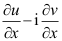
答案: 【

】

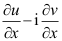
5、 问题:

下列关于复积分性质的描述中哪些是正确的（ ）

选项：
A:函数的和的积分等于各个函数的积分之和
B:反转积分路径，积分变号
C:全路径上的积分等于各段上的积分之和

D:实积分的所有性质复积分都适用

答案: 【
函数的和的积分等于各个函数的积分之和
反转积分路径，积分变号
全路径上的积分等于各段上的积分之和

】

6、 问题:关于复变函数的积分，下面哪些说法是正确的（ ）？
选项：
A:复变函数的积分不仅跟被积函数有关，也跟积分路径有关
B:被积函数相同时，积分路径不同，积分结果一定不同
C:对于复变函数的积分，牛顿-莱布尼兹公式同样适用
D:函数f(z)在某个单通区域B内解析，则B内任意阶导数都存在
答案: 【
复变函数的积分不仅跟被积函数有关，也跟积分路径有关
函数f(z)在某个单通区域B内解析，则B内任意阶导数都存在
】

7、 问题:关于复通区域的柯西定理，下列哪些说法是正确的（ ）？
选项：
A:复通区域上的解析函数沿所有内外边界线正方向的积分和为0
B:复通区域上的解析函数沿外边界线逆时针方向的积分等于沿所有内边界线逆时针方向的积分之和
C:复通区域上解析的函数其任意阶导数都存在
D:定理成立的前提条件是函数f(z)在复通区域B上解析，在闭复通区域 上连续
答案: 【
复通区域上的解析函数沿所有内外边界线正方向的积分和为0
复通区域上的解析函数沿外边界线逆时针方向的积分等于沿所有内边界线逆时针方向的积分之和
定理成立的前提条件是函数f(z)在复通区域B上解析，在闭复通区域 上连续
】

8、 问题:

单通区域上，复积分的值与路径无关。

选项：
A:对
B:错
答案: 【
错
】

9、 问题:区域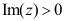 是无界的单连通的闭区域。（ ）
选项：
A:对
B:错
答案: 【
错
】

10、 问题:柯西公式表明解析函数可以用沿区域边界线的积分表示。（ ）
选项：
A:对
B:错
答案: 【
对
】

11、 问题:高阶导数公式是复通区域柯西公式的重要推广。（ ）
选项：
A:对
B:错
答案: 【
错
】

12、 问题:级数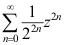 的收敛半径为（ ）。
选项：
A:0
B:1
C:2
D:3
答案: 【
2
】

第三章 单元测试

1、 问题:设级数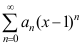 的收敛半径为1，则级数在x=3点（ ）。
选项：
A:发散
B:条件收敛
C:绝对收敛
D:不能确定敛散性
答案: 【
发散
】

绪论 单元测试

1、 问题:

点解析和点可导是等价的。（ ）