2020 算法设计与分析(广西科技大学启迪数字学院) 最新满分章节测试答案

文章目录[隐藏]

第二周基础知识（2）：序列求和方法，递推方程求解作业测验
第三周分治策略（1）作业测验
第四周分治策略（2）作业测验
第五周动态规划（1）作业测验
第六周动态规划（2）作业测验

本答案对应课程为:点我自动跳转查看
本课程起止时间为:2020-04-20到2020-07-10
本篇答案更新状态:已完结

第二周基础知识（2）：序列求和方法，递推方程求解作业测验

1、问题:递归方程的解的精确值是：
选项：
A:
B:
C:
D:
E:
F:
答案: 【】

2、问题:，的阶是：
选项：
A:
B:
C:
D:
E:
F:
答案: 【】

3、问题:请用主定理确定递归式的渐近的界：
选项：
A:
B:
C:
D:
E:
答案: 【】

4、问题:给定个数的数组，其中，为非负整数，求中的最大数. 考虑下述算法A，先把数组从中间划分成两个个数的数组和，在和中用同样的算法通过数之间的比较运算找最大数，如果的最大数是,的最大数是,那么就是问题的解。假设对于个数的数组，在最坏情况下算法A的比较次数是，该算法在最坏情况下的递推方程是：
选项：
A:
B:
C:
D:
E:
F:
答案: 【】

5、问题:给定个数的数组，其中，为非负整数，求中的最大数. 考虑下述算法A，先把数组从中间划分成两个个数的数组和，在和中用同样的算法通过数之间的比较运算找最大数，如果的最大数是,的最大数是,那么就是问题的解。假设对于个数的数组，在最坏情况下算法A的比较次数是，则的精确值是？
选项：
A:
B:
C:
D:
E:
F:
答案: 【】

6、问题:把插入排序算法加以改进，可以得到二分插入排序算法。设输入数组是，插入排序算法的基本操作是：假定的前个数已经排好，将插入。插入时从开始，顺序检查，直到找到插入的合适的位置，将它插入。改进插入排序算法的步骤是：插入的操作不是在中从后向前顺序检索，而是采用二分检索方法找到插入的正确位置。如果输入规模是，该算法在最坏情况下的比较次数是，那么该算法在最坏情况下的递推方程是
选项：
A:
B:
C:
D:
E:
答案: 【】

7、问题:把插入排序算法加以改进，可以得到二分插入排序算法。设输入数组是，插入排序算法的基本操作是：假定的前个数已经排好，将插入。插入时从开始，顺序检查，直到找到插入的合适的位置，将它插入。改进插入排序算法的步骤是：插入的操作不是在中从后向前顺序检索，而是采用二分检索方法找到插入的正确位置。如果输入规模是，该算法在最坏情况下的比较次数是，那么该算法在最坏情况下的递推方程的解是？
选项：
A:
B:
C:
D:
E:
F:
答案: 【】

8、问题:设递推方程给出了算法A在最坏情况下的时间复杂度函数，算法B在最坏情况下的时间复杂度函数满足递推方程，那么要使算法B比算法A具有更高的效率，即时间复杂度的阶低于的阶的最大正整数的值为：
答案: 【48】

9、问题:给定个数的数组，其中，为非负整数，求中的最大数. 考虑下述算法A，先把数组从中间划分成两个个数的数组和，在和中用同样的算法通过数之间的比较运算找最大数，如果的最大数是,的最大数是,那么就是问题的解。假设对于个数的数组，在最坏情况下算法A的比较次数是，则的初值是（）？
答案: 【0】

10、问题:把插入排序算法加以改进，可以得到二分插入排序算法。设输入数组是，插入排序算法的基本操作是：假定的前个数已经排好，将插入。插入时从开始，顺序检查，直到找到插入的合适的位置，将它插入。改进插入排序算法的步骤是：插入的操作不是在中从后向前顺序检索，而是采用二分检索方法找到插入的正确位置。如果输入规模是，该算法在最坏情况下的比较次数是，那么该算法在最坏情况下的递推方程的初值是（）？
答案: 【0】

第三周分治策略（1）作业测验

1、问题:双Hanoi塔问题是Hanoi塔问题的一种推广，与Hanoi塔的不同点在于：2n个圆盘，分成大小不同的n对，每对圆盘完全相同。初始，这些圆盘按照从大到小的次序从下到上放在A柱上，最终要把它们全部移到C柱，移动的规则与Hanoi塔相同。BiHanoi(A, C, n)的功能是从A移动2n个盘子到C，其中BiMove(A, C)表示从A移动两个盘子到C。下列哪一段代码是利用分治策略给出的正确的移动策略：
选项：
A:
B:
C:
D:
答案: 【】

2、问题:给定n个不同数的数组S和正整数i，，求S中最大的i个数，并且按照从大到小的次序输出，现有如下算法，算法：调用i次找最大算法Findmax，每次从S中删除一个最大的数。该算法在最坏情况下的时间复杂度是：
选项：
A:
B:
C:
D:
E:
答案: 【】

3、问题:给定n个不同数的数组S和正整数i，，求S中最大的i个数，并且按照从大到小的次序输出，现有如下算法，算法：对S排序，并输出S中最大的i个数。该算法在最坏情况下的时间复杂度是：
选项：
A:
B:
C:
D:
E:
F:
答案: 【】

4、问题:有n个砝码（其中n为2的幂，即），每个重g克，其中一个不合格(重量可能大于或小于g克). 有一个秤可以称出重物的准确重量. 假设所有的砝码可以同时放到秤上，设计一个算法找出这个不合格的砝码，且秤重的次数达到最少. 采用分治算法，每次取一半砝码（比如t个）称重，如果恰好重tg克，那么不合格的砝码在剩下的砝码中；否则不合格的砝码就在被称重的砝码中. 设n枚砝码的称重次数是T(n)，关于T(n)的递推方程是:括号里应该填：
选项：
A:
B:
C:
D:
E:
答案: 【】

5、问题:在之前n个砝码的题目中（其顺序可能出现在该题之后），在初值T(2)=1条件下，确定：对于给定的n个砝码，找到其中不合格砝码最多需要称重多少次，并选择一个函数填入括号内. .
选项：
A:
B:
C:
D:
E:
答案: 【】

6、问题:设问题P的输入规模是n，下述三个算法是求解P的不同的分治算法. 算法1：在常数时间将原问题划分为规模减半的5个子问题，递归求解每个子问题，最多用线性时间将子问题的解综合而得到原问题的解. 算法2：先递归求解2个规模为n-1的子问题，最多用常量时间将子问题的解综合得到原问题的解. 算法3：在常数时间将原问题划分为规模n/3的9个子问题，递归求解每个子问题，最多用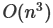时间将子问题的解综合得到原问题的解. 要求在上述三个算法中选择最坏情况下时间复杂度最低的算法，需要选择哪个算法？
选项：
A:1
B:2
C:3
D:都不对
答案: 【1】

7、问题:设问题P的输入规模是n，下述三个算法是求解P的不同的分治算法. 算法1：在常数时间将原问题划分为规模减半的5个子问题，递归求解每个子问题，最多用线性时间将子问题的解综合而得到原问题的解. 算法2：先递归求解2个规模为n-1的子问题，最多用常量时间将子问题的解综合得到原问题的解. 算法3：在常数时间将原问题划分为规模n/3的9个子问题，递归求解每个子问题，最多用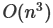时间将子问题的解综合得到原问题的解. 设最坏情况下时间复杂度最低的算法为A，A在最坏情况下的时间复杂度是
选项：
A:
B:
C:
D: